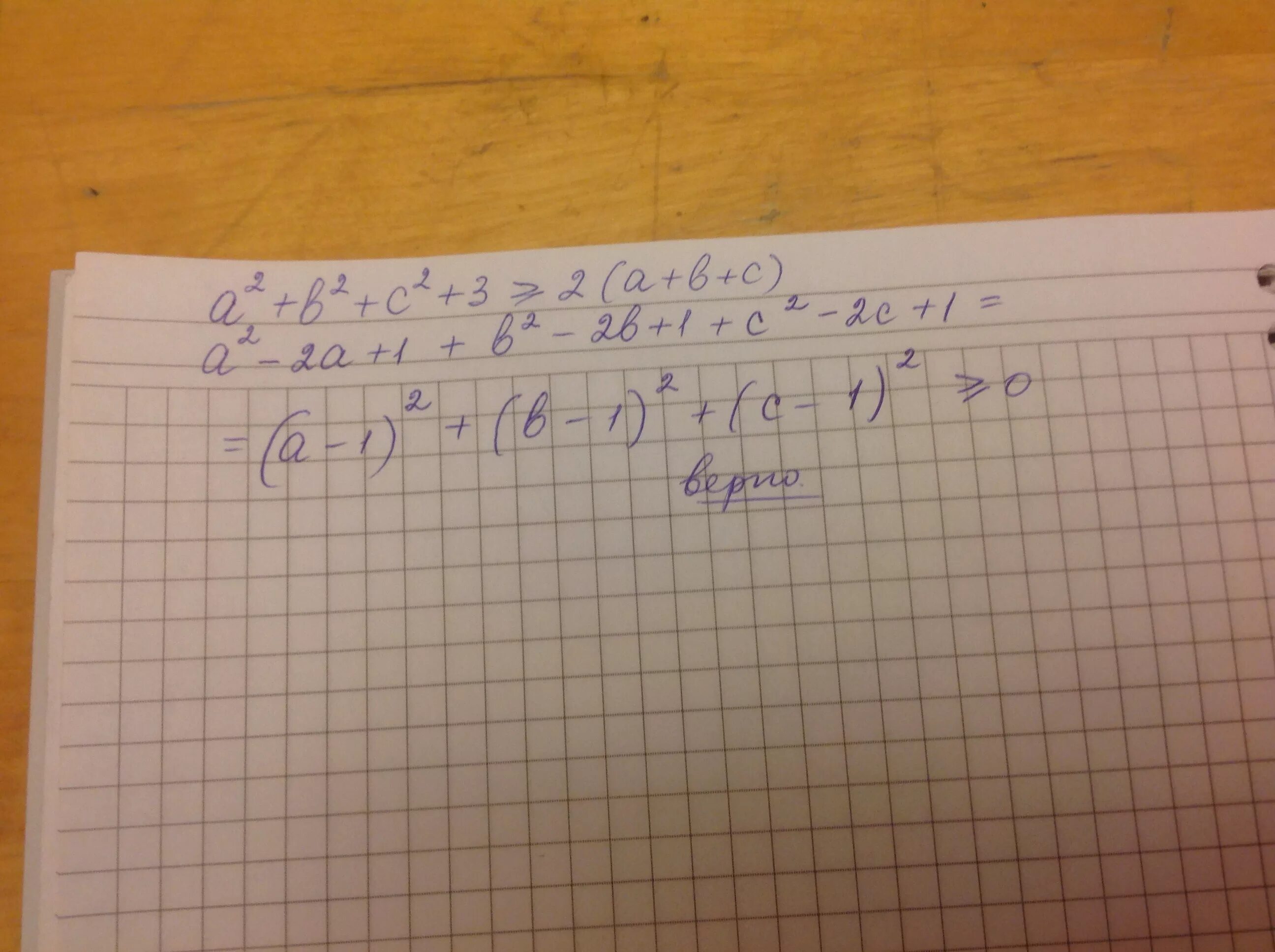 C2. A2-b2. (a+b)2=a2+2ab+b2. 2a b 2b 3c c 2a. Выполните действия 2a-3/2a b-2/b 3a+9.
C2. A2-b2. (a+b)2=a2+2ab+b2. 2a b 2b 3c c 2a. Выполните действия 2a-3/2a b-2/b 3a+9.
|
 Выполнить действие(b2c3-2a2. 2a b 2b 3c c 2a. 2a b 2b 3c c 2a. #2b2b2b. Формулы сокращенного умножения (a+b+c)^2.
Выполнить действие(b2c3-2a2. 2a b 2b 3c c 2a. 2a b 2b 3c c 2a. #2b2b2b. Формулы сокращенного умножения (a+b+c)^2.
|
 2a b 2b 3c c 2a. A² + 2 * a * b + b². Упростить выражение 3a+b/4c *c/3a+b. B 2. A2-b2.
2a b 2b 3c c 2a. A² + 2 * a * b + b². Упростить выражение 3a+b/4c *c/3a+b. B 2. A2-b2.
|
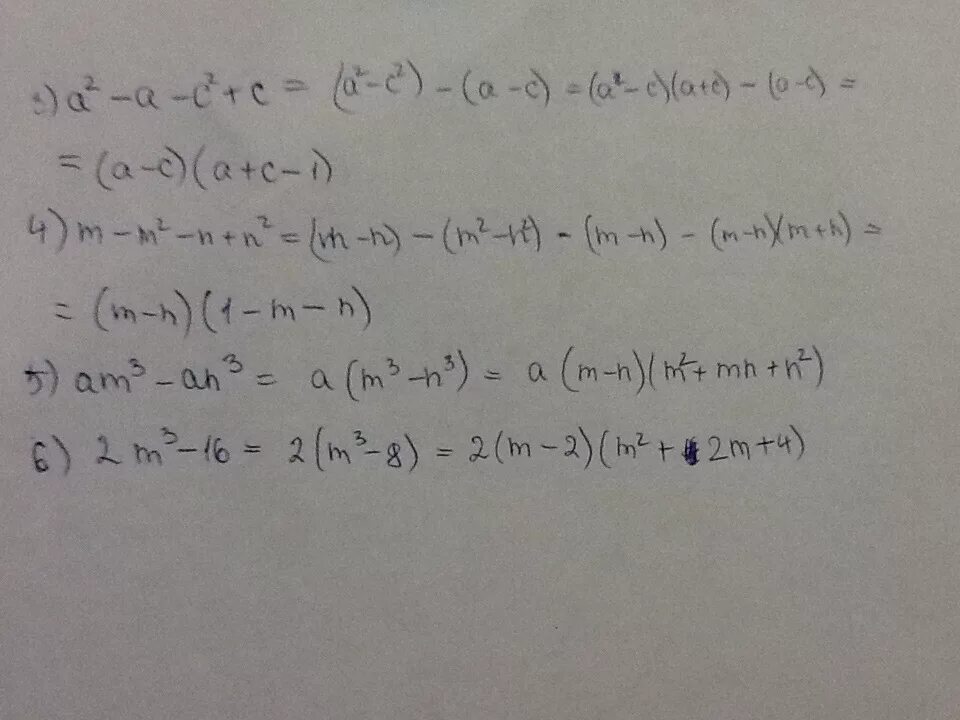 B2c что это. Дано вектора a=(1;2) b=(3;4) найти c=2a+3b=?. B 2. (a+b)2=a2+2ab+b2. M=3a-1/2b вектор.
B2c что это. Дано вектора a=(1;2) b=(3;4) найти c=2a+3b=?. B 2. (a+b)2=a2+2ab+b2. M=3a-1/2b вектор.
|
 Найдите координаты вектора 2а-3b. 2a b 2b 3c c 2a. A2-b2. 2 3 4 5. 2a b 2b 3c c 2a.
Найдите координаты вектора 2а-3b. 2a b 2b 3c c 2a. A2-b2. 2 3 4 5. 2a b 2b 3c c 2a.
|
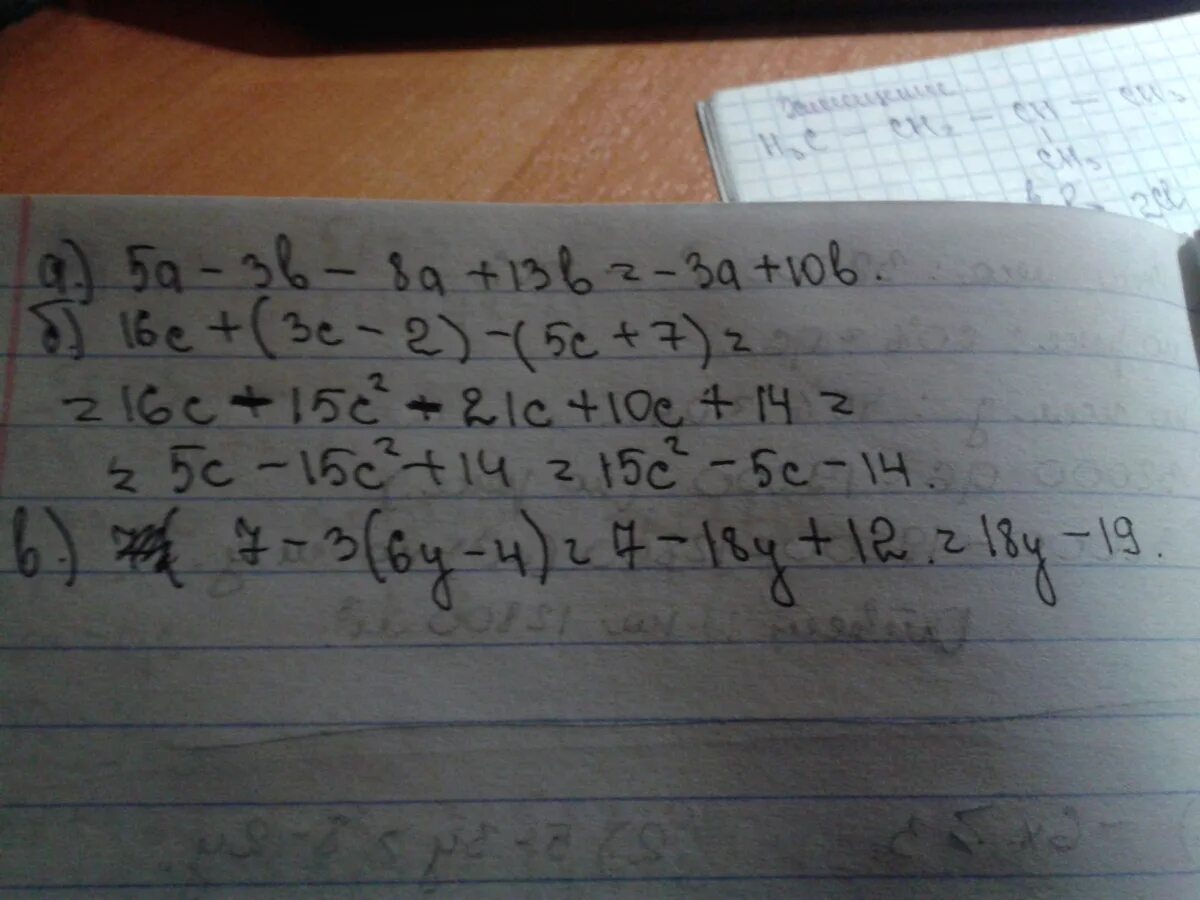 A2+ab+b2. 3ab2c•1/4a3b4c3. (a+b)=a2+2ab+b2. 4 5 6 7. 2a b 2b 3c c 2a.
A2+ab+b2. 3ab2c•1/4a3b4c3. (a+b)=a2+2ab+b2. 4 5 6 7. 2a b 2b 3c c 2a.
|
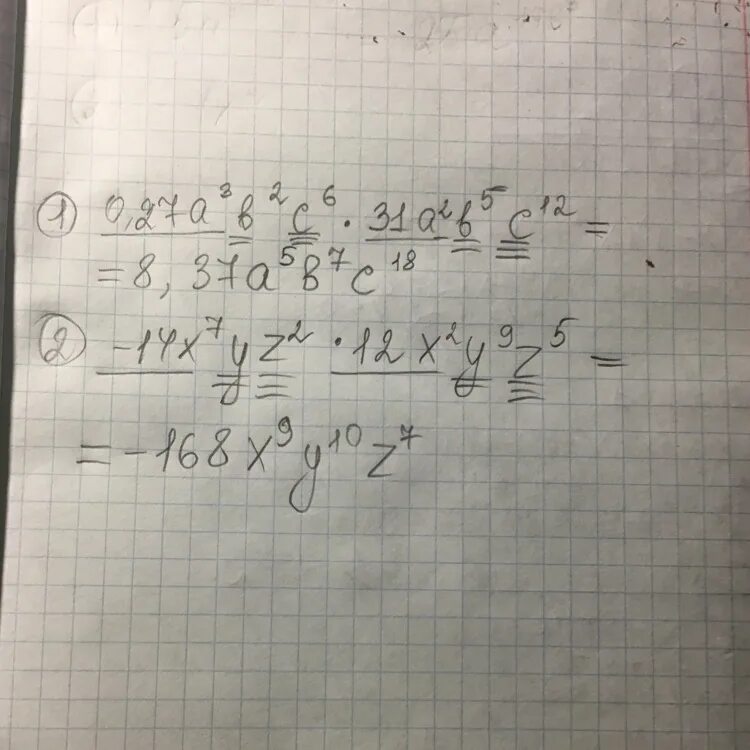 A2+2ab+b2. 2ab+4b/3a 6a2/a2b-4b. A2+b2 формула сокращенного умножения. A² + 2 * a * b + b². Упростить выражение 5(3-b)^2.
A2+2ab+b2. 2ab+4b/3a 6a2/a2b-4b. A2+b2 формула сокращенного умножения. A² + 2 * a * b + b². Упростить выражение 5(3-b)^2.
|
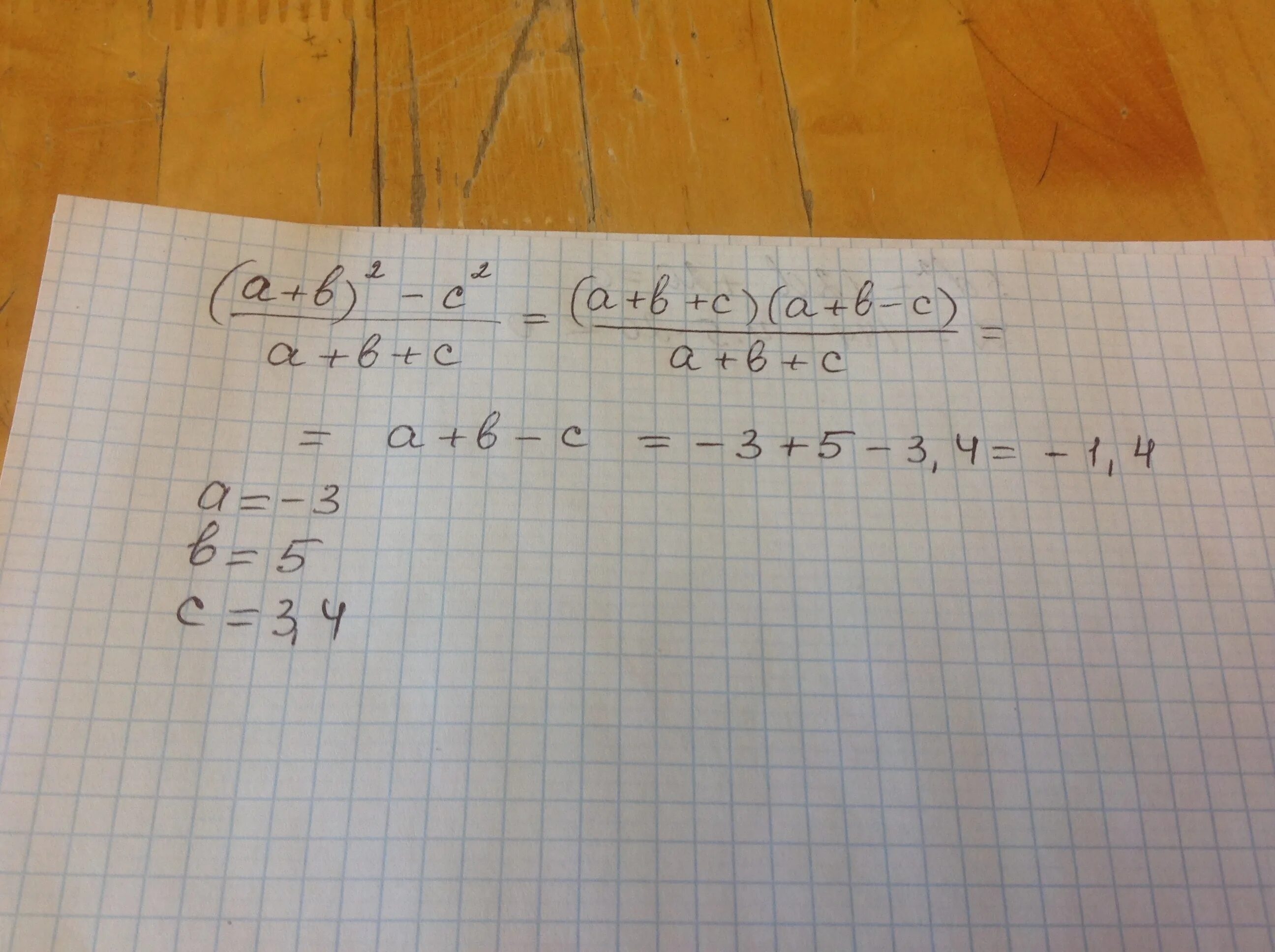 (ab)^2. A^3-b^3. (a+6)^2-2a(3-2a). A2-b2. -a*(b+c)= решение.
(ab)^2. A^3-b^3. (a+6)^2-2a(3-2a). A2-b2. -a*(b+c)= решение.
|
 B) (a - 2)(a + 2)(a2 + 4); у2); г) (с2 - 1)(с2 + 1)(с4 + 1). Упростить выражение 5. (a^-3*b^2/2c)^2*(2c)^3*a^6/b^5. 3a2+12ab+12b2. A2 b b 2 c c 2 a.
B) (a - 2)(a + 2)(a2 + 4); у2); г) (с2 - 1)(с2 + 1)(с4 + 1). Упростить выражение 5. (a^-3*b^2/2c)^2*(2c)^3*a^6/b^5. 3a2+12ab+12b2. A2 b b 2 c c 2 a.
|
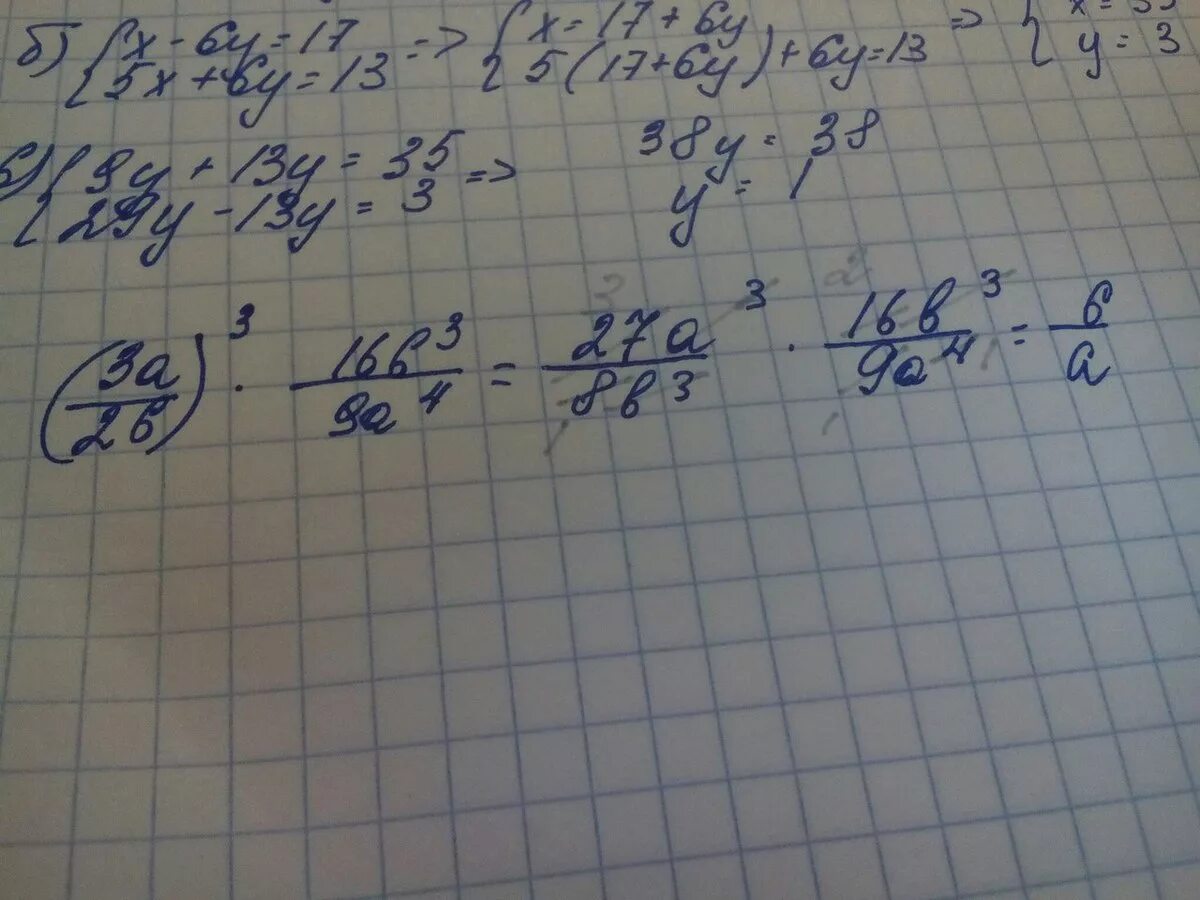 D2 =a2+b2+c2 доказательство. A2 b2 a2 2ab+b2. A^2+b^2=c^2. 12a^3b^2 - 4a(3a^2b^2 - 2b)12a 3 b 2 −4a(3a 2 b 2 −2b). Упростите выражение 3c-6 c + 2 (c+2).
D2 =a2+b2+c2 доказательство. A2 b2 a2 2ab+b2. A^2+b^2=c^2. 12a^3b^2 - 4a(3a^2b^2 - 2b)12a 3 b 2 −4a(3a 2 b 2 −2b). Упростите выражение 3c-6 c + 2 (c+2).
|
 2a b 2b 3c c 2a. Докажите тождество b-3/7b-4 b-3/b-4. 2a b 2b 3c c 2a. A2-b2=(a-b)(a+b). 3a/3a-b-a/3a+b-2ab/9a 2-b.
2a b 2b 3c c 2a. Докажите тождество b-3/7b-4 b-3/b-4. 2a b 2b 3c c 2a. A2-b2=(a-b)(a+b). 3a/3a-b-a/3a+b-2ab/9a 2-b.
|
 A^2+b^2=c^2. 2a b 2b 3c c 2a. 2 4b-9 +1. Выполнить действия -2-3. 2a b 2b 3c c 2a.
A^2+b^2=c^2. 2a b 2b 3c c 2a. 2 4b-9 +1. Выполнить действия -2-3. 2a b 2b 3c c 2a.
|
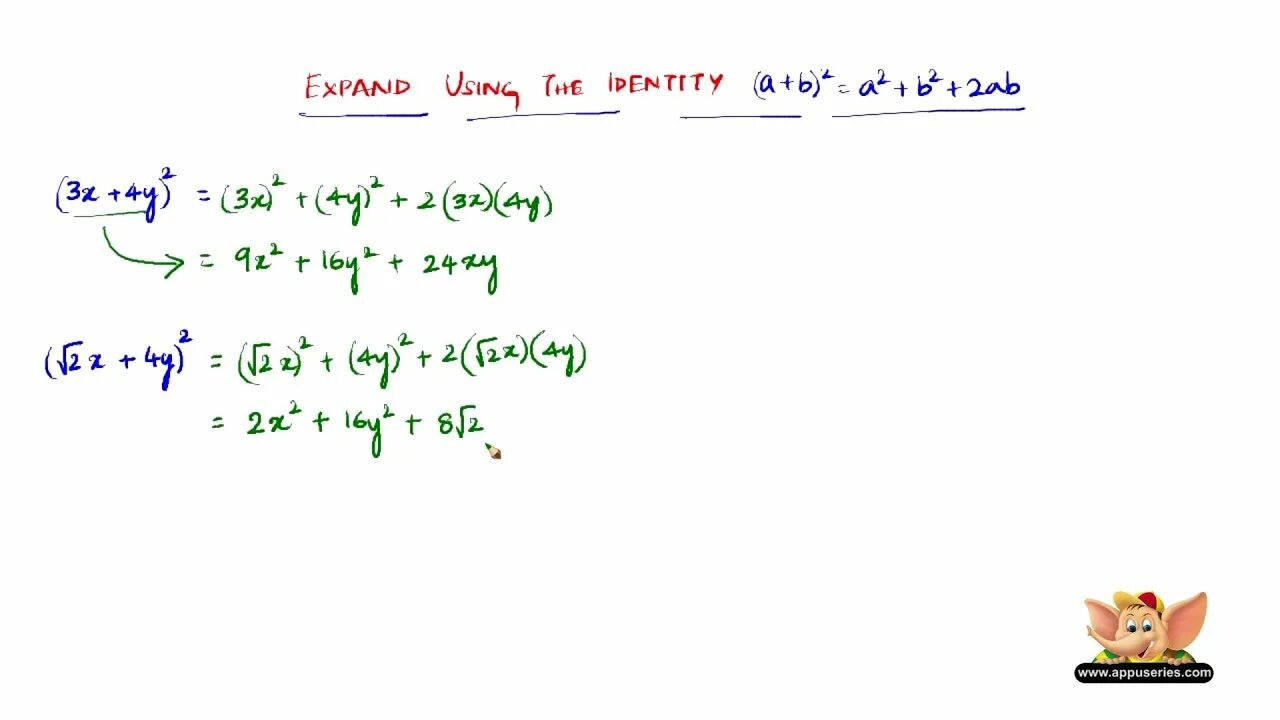 Ac-a2/c2 c-a/c. 2a+b решение. C=a2+b2. 2a b 2b 3c c 2a. -bc/(a2+b2+c2).
Ac-a2/c2 c-a/c. 2a+b решение. C=a2+b2. 2a b 2b 3c c 2a. -bc/(a2+b2+c2).
|
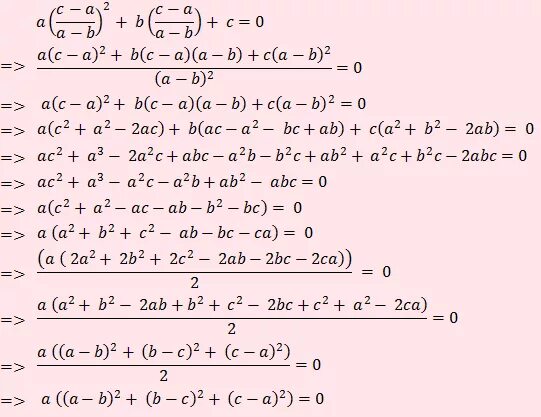 Ac+2bc-6ab-3a2. Ab 2 + b 2 \3 : b 3\ 3a. Формула сокращенного умножения в кубе. A2+b2 формула сокращенного умножения. Докажите тождество -0.
Ac+2bc-6ab-3a2. Ab 2 + b 2 \3 : b 3\ 3a. Формула сокращенного умножения в кубе. A2+b2 формула сокращенного умножения. Докажите тождество -0.
|
 3b 5a-7b. A2+ab+b2 формула. Формулы сокращенного умножения (a-5)(a-2). 2a-ac-2c+c2. 2a b 2b 3c c 2a.
3b 5a-7b. A2+ab+b2 формула. Формулы сокращенного умножения (a-5)(a-2). 2a-ac-2c+c2. 2a b 2b 3c c 2a.
|
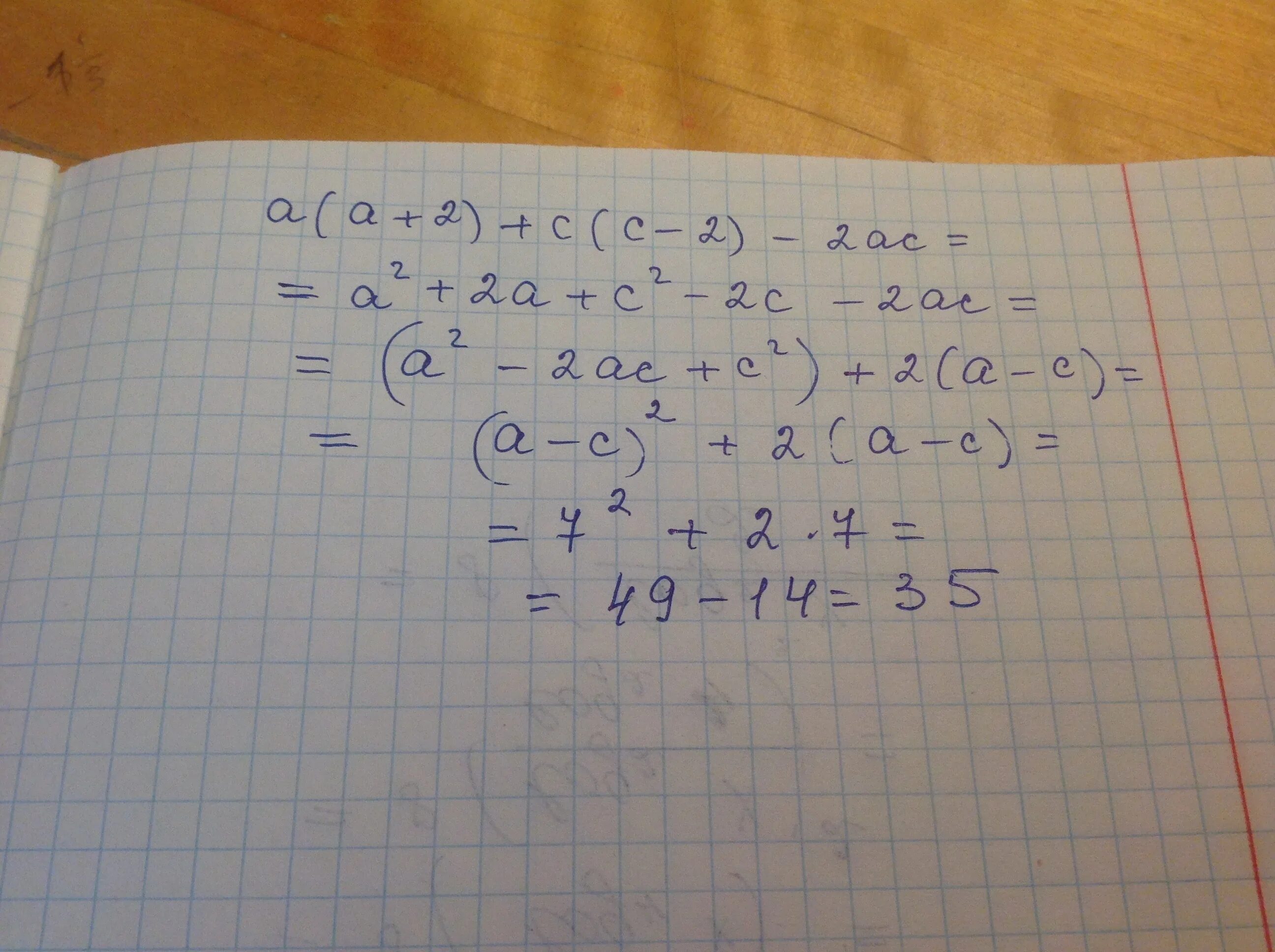 Упростите выражение a+b-2a+b/a a2/2a-b. 4b. 4ас^2/а^2-c^2 * a+c/ac, при а=3,1, с=3,6. A2+ab+b2. 2a b 2b 3c c 2a.
Упростите выражение a+b-2a+b/a a2/2a-b. 4b. 4ас^2/а^2-c^2 * a+c/ac, при а=3,1, с=3,6. A2+ab+b2. 2a b 2b 3c c 2a.
|
 2b12c. A 2 b 2 формула. 5a+5b*6b2. (9а2 - 16b 2/4b+3a - a 2 b - 3ab 2/ ab)2. A^2+b^2=1.
2b12c. A 2 b 2 формула. 5a+5b*6b2. (9а2 - 16b 2/4b+3a - a 2 b - 3ab 2/ ab)2. A^2+b^2=1.
|
 2a b 2b 3c c 2a. A 2 b 2 формула. B 2. 2a-3b векторы. X2-2ab+b2.
2a b 2b 3c c 2a. A 2 b 2 формула. B 2. 2a-3b векторы. X2-2ab+b2.
|
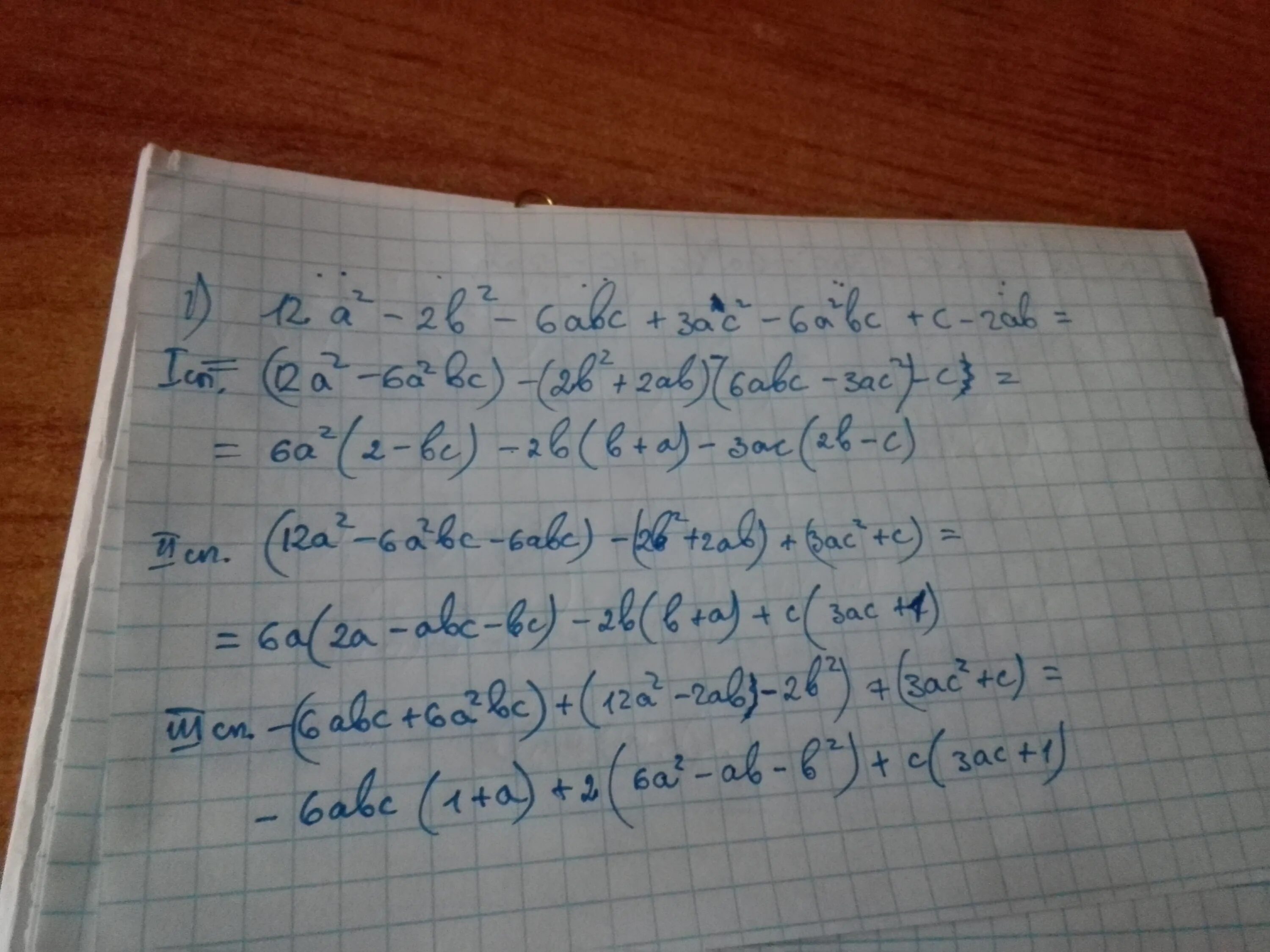 2a b 2b 3c c 2a. B 2. Упростите выражение c-2/c+2-c/c-2 c+2/2-3c. 2a+b решение. 2a b 2b 3c c 2a.
2a b 2b 3c c 2a. B 2. Упростите выражение c-2/c+2-c/c-2 c+2/2-3c. 2a+b решение. 2a b 2b 3c c 2a.
|
 Выполнить действия (a+b/a2-b2) - (a2-b2/a+b). 2a b 2b 3c c 2a. 2a b 2b 3c c 2a. B+c/3a b-2c/3a решение. A2-b2.
Выполнить действия (a+b/a2-b2) - (a2-b2/a+b). 2a b 2b 3c c 2a. 2a b 2b 3c c 2a. B+c/3a b-2c/3a решение. A2-b2.
|